IASbaba’s Daily CSAT Practice Test
ARCHIVES
Daily CSAT Practice Test
Everyday 5 Questions from Aptitude, Logical Reasoning, and Reading Comprehension will be covered from Monday to Saturday.
Make the best use of the initiative. All the best!
To Know More about Ace the Prelims (ATP) 2021 – CLICK HERE
Important Note:
- Don’t forget to post your marks in the comment section. Also, let us know if you enjoyed today’s test 🙂
- After completing the 5 questions, click on ‘View Questions’ to check your score, time taken and solutions.
Test-summary
0 of 5 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
Information
To view Solutions, follow these instructions:
- Click on – ‘Start Test’ button
- Solve Questions
- Click on ‘Test Summary’ button
- Click on ‘Finish Test’ button
- Now click on ‘View Questions’ button – here you will see solutions and links.
You have already completed the test before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the test.
You have to finish following test, to start this test:
Results
0 of 5 questions answered correctly
Your time:
Time has elapsed
You have scored 0 points out of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- Answered
- Review
-
Question 1 of 5
1. Question
The difference of two numbers is 1365. On dividing the larger number by the smaller, 6 is obtained as quotient and 15 as remainder. What is the smaller number?
Correct
Solution (a)
Let the smaller number be x and the larger number be ( x + 1365)
( x + 1365 ) ÷ x = 6, remainder = 15
(x + 1365) / x = 6, remainder = 15
(x + 1365) = 6x + 15
5x = 1350, x = 270
Smaller number = x = 270
Incorrect
Solution (a)
Let the smaller number be x and the larger number be ( x + 1365)
( x + 1365 ) ÷ x = 6, remainder = 15
(x + 1365) / x = 6, remainder = 15
(x + 1365) = 6x + 15
5x = 1350, x = 270
Smaller number = x = 270
-
Question 2 of 5
2. Question
Find the missing number from the following pattern
Correct
Solution (b)
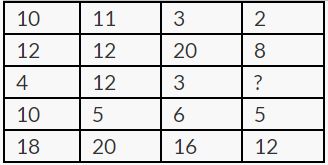
Column One: (10 +12+4+10) /2 = 18
Column Two: (11 +12 +5+20) /2 = 20
In the same way column four: (2+8+9+5)/ 2 = 12
Incorrect
Solution (b)

Column One: (10 +12+4+10) /2 = 18
Column Two: (11 +12 +5+20) /2 = 20
In the same way column four: (2+8+9+5)/ 2 = 12
-
Question 3 of 5
3. Question
A student divides a number by 5 and gets 3 as remainder. If his friend divides the square of the number by 5, what will be the remainder?
Correct
Solution (a)
Let P be the number
Let P/5 = a and the remainder = 3
Then P = 5a + 3
P2 = (5a + 3)2
= (5a)2 + (2*5a*3) + 9
= 25a2 + 30a + 5 + 4
= 5(5a2 + 6a + 1) + 4
Hence if P2 is divided by 5, we will get 4 as a remainder.
Incorrect
Solution (a)
Let P be the number
Let P/5 = a and the remainder = 3
Then P = 5a + 3
P2 = (5a + 3)2
= (5a)2 + (2*5a*3) + 9
= 25a2 + 30a + 5 + 4
= 5(5a2 + 6a + 1) + 4
Hence if P2 is divided by 5, we will get 4 as a remainder.
-
Question 4 of 5
4. Question
10 men working 9 hours a day can complete a work in 24 days. How much time will it take to complete the work if 15 men are employed for 6 hours a day?
Correct
Solution (c)
We know that M1 D1 H1 E1 / W1 = M2 D2 H2 E2 / W2, where
M1 = 10 men D1 = 24 days H1 = 9 hours/day
W1 = W2 = Work to be done
E1 = E2 = Efficiency of each man
M2 = 15 men D2 = Days required by 15 men H2 = 6 hours/day
So, we have
10 x 24 x 9 = 15 x 6 x D2
=> D2 = 24
Therefore, 15 men working 6 hours / day would require 24 days to complete the work.
Incorrect
Solution (c)
We know that M1 D1 H1 E1 / W1 = M2 D2 H2 E2 / W2, where
M1 = 10 men D1 = 24 days H1 = 9 hours/day
W1 = W2 = Work to be done
E1 = E2 = Efficiency of each man
M2 = 15 men D2 = Days required by 15 men H2 = 6 hours/day
So, we have
10 x 24 x 9 = 15 x 6 x D2
=> D2 = 24
Therefore, 15 men working 6 hours / day would require 24 days to complete the work.
-
Question 5 of 5
5. Question
Suresh, David and Jai completed a work together in 36 days and received a total payment of Rs 54000. Suresh took half of the total money, David took one third and Jai took remaining. In how many days, Suresh and Jai would have finished the work if David was not working?
Correct
Solution (a)
Suresh, David and Jai completed a work together in 36 days.
In one day, together they will finish 1/36 of work.
Out of Rs 54000, Suresh took half of the total money, David took one third and Jai took remaining.
Incorrect
Solution (a)
Suresh, David and Jai completed a work together in 36 days.
In one day, together they will finish 1/36 of work.
Out of Rs 54000, Suresh took half of the total money, David took one third and Jai took remaining.











