IASbaba’s Daily CSAT Practice Test
ARCHIVES
Daily CSAT Practice Test
Everyday 5 Questions from Aptitude, Logical Reasoning, and Reading Comprehension will be covered from Monday to Saturday.
Make the best use of the initiative. All the best!
To Know More about Ace the Prelims (ATP) 2021 – CLICK HERE
Important Note:
- Don’t forget to post your marks in the comment section. Also, let us know if you enjoyed today’s test 🙂
- After completing the 5 questions, click on ‘View Questions’ to check your score, time taken and solutions.
Test-summary
0 of 5 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
Information
To view Solutions, follow these instructions:
- Click on – ‘Start Test’ button
- Solve Questions
- Click on ‘Test Summary’ button
- Click on ‘Finish Test’ button
- Now click on ‘View Questions’ button – here you will see solutions and links.
You have already completed the test before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the test.
You have to finish following test, to start this test:
Results
0 of 5 questions answered correctly
Your time:
Time has elapsed
You have scored 0 points out of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- Answered
- Review
-
Question 1 of 5
1. Question
What will be the number of zeroes at the end of the product of the first 100 natural numbers?
Correct
Solution (a)
In these kinds of questions, one needs to find greatest power of 5, which can divide the product of the first 100 natural numbers. Remember, a multiple of 5 multiplied by any even number, gives you a zero. Now divide 100 by 5 and take 20 as quotient. Then divide 20 (the quotient) by 5 and get the new quotient 4, which further cannot be divided by 5. The sum of all such quotient gives you the greatest power of 5, which can divide that number. The sum is 24 and this is the number of zeroes at the end of the product of the first 100 natural numbers.
Incorrect
Solution (a)
In these kinds of questions, one needs to find greatest power of 5, which can divide the product of the first 100 natural numbers. Remember, a multiple of 5 multiplied by any even number, gives you a zero. Now divide 100 by 5 and take 20 as quotient. Then divide 20 (the quotient) by 5 and get the new quotient 4, which further cannot be divided by 5. The sum of all such quotient gives you the greatest power of 5, which can divide that number. The sum is 24 and this is the number of zeroes at the end of the product of the first 100 natural numbers.
-
Question 2 of 5
2. Question
Sundar, Ganesh and Mahesh are three partners in a business. Their capitals are respectively Rs 4,000, Rs 8,000 and Rs 6,000. Sundar gets 20% of total profit for managing the business. The remaining profit is divided among the three in the ratio of their capitals. At the end of the year, the profit of Sundar is Rs 2,200 less than the sum of the profit of Ganesh and Mahesh. How much profit did Mahesh get?
Correct
Solution (b)
Let the total profit be P Rs. Sundar will get 0.2P for managing the business and rest 0.8 P will be divided in the ratio of 2:4:3
i.e. Sundar will get 0.2P+0.8P*2/9 and Ganesh and Mahesh will together get 0.8P*7/9
Given that 0.8P*7/9 – (0.2P+0.8P* 2/9) = 2200
Solving we get P = 9000 Rs
Therefore profit Mahesh will get is 2400 Rs
Therefore option b is correct.
Incorrect
Solution (b)
Let the total profit be P Rs. Sundar will get 0.2P for managing the business and rest 0.8 P will be divided in the ratio of 2:4:3
i.e. Sundar will get 0.2P+0.8P*2/9 and Ganesh and Mahesh will together get 0.8P*7/9
Given that 0.8P*7/9 – (0.2P+0.8P* 2/9) = 2200
Solving we get P = 9000 Rs
Therefore profit Mahesh will get is 2400 Rs
Therefore option b is correct.
-
Question 3 of 5
3. Question
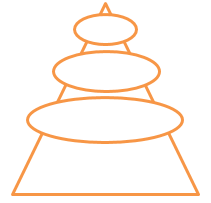
In the following figure, the smallest cone has a base radius of 2 cm and a height of 1 cm. The heights of successive cones from the top form a Geometric Progression with 1 as the first term and 3 as the common ratio. What shall be the ratio of the volumes of the smallest cone, to the two following bigger cones?
 Correct
Correct
Solution (d)
We get the heights of the successive cones as 1, 3 and 9.
In Geometric Progression, If the first term is 1 and common ratio is 3, the series will be 1, 3, 9…so on
Here we have only 3 cones, so their heights will be 1, 3 and 9
Since the base radii will increase in the same proportion as the heights, the volumes will be proportional to the cubes of the height (because volume = radius2 x height).
So the ratio of the volumes will be 13 : 33 : 93 = 1 : 27 : 729.
Incorrect
Solution (d)
We get the heights of the successive cones as 1, 3 and 9.
In Geometric Progression, If the first term is 1 and common ratio is 3, the series will be 1, 3, 9…so on
Here we have only 3 cones, so their heights will be 1, 3 and 9
Since the base radii will increase in the same proportion as the heights, the volumes will be proportional to the cubes of the height (because volume = radius2 x height).
So the ratio of the volumes will be 13 : 33 : 93 = 1 : 27 : 729.
-
Question 4 of 5
4. Question
Which of the following number is wrong in the following series?
150, 290, 560, 1120, 2140, 4230, 8400
Correct
Solution (b)
The series follows the below pattern
150*2 – 10 = 290
290*2 – 20 = 560
560*2 – 30 = 1090
1090*2 – 40 = 2140
2140*2 – 50 = 4230
4230*2 – 60 = 8400
Hence, we see that 1090 should come in place of 1120
Incorrect
Solution (b)
The series follows the below pattern
150*2 – 10 = 290
290*2 – 20 = 560
560*2 – 30 = 1090
1090*2 – 40 = 2140
2140*2 – 50 = 4230
4230*2 – 60 = 8400
Hence, we see that 1090 should come in place of 1120
-
Question 5 of 5
5. Question
Which of the following number is wrong in the following series?
29, 37, 21, 43, 13, 53, 5
Correct
Solution (c)
The following series can be divided into 2 parts
Odd place numbers decreases by 8 and even place numbers increases by 8 successively
So, 29 – 8 = 21, 21 – 8 = 13, 13 – 8 = 5
Likewise, 37 + 8 = 45
45 + 8 = 53 so on
Therefore, it should be 45 instead of 43 hence 43 is wrong number
Incorrect
Solution (c)
The following series can be divided into 2 parts
Odd place numbers decreases by 8 and even place numbers increases by 8 successively
So, 29 – 8 = 21, 21 – 8 = 13, 13 – 8 = 5
Likewise, 37 + 8 = 45
45 + 8 = 53 so on
Therefore, it should be 45 instead of 43 hence 43 is wrong number












