IASbaba’s Daily CSAT Practice Test
ARCHIVES
Daily CSAT Practice Test
Everyday 5 Questions from Aptitude, Logical Reasoning, and Reading Comprehension will be covered from Monday to Saturday.
Make the best use of the initiative. All the best!
To Know More about Ace the Prelims (ATP) 2021 – CLICK HERE
Important Note:
- Don’t forget to post your marks in the comment section. Also, let us know if you enjoyed today’s test 🙂
- After completing the 5 questions, click on ‘View Questions’ to check your score, time taken and solutions.
Test-summary
0 of 5 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
Information
To view Solutions, follow these instructions:
- Click on – ‘Start Test’ button
- Solve Questions
- Click on ‘Test Summary’ button
- Click on ‘Finish Test’ button
- Now click on ‘View Questions’ button – here you will see solutions and links.
You have already completed the test before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the test.
You have to finish following test, to start this test:
Results
0 of 5 questions answered correctly
Your time:
Time has elapsed
You have scored 0 points out of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- Answered
- Review
-
Question 1 of 5
1. Question
In a traffic signal red light flashes 7 times per minute and the green light flashes 13 times in 2 minutes at regular intervals. If both the lights start flashing at the same time, how many times do they flash together in an hour?
Correct
Solution (c)
First light flashes after 60/7 sec
Second light flashes after 120/13 sec they blink together after
(LCM of 60/7 , 120/13) = 120sec = 2 min,
So in one hour they blink together = 60/2=30 times.
Incorrect
Solution (c)
First light flashes after 60/7 sec
Second light flashes after 120/13 sec they blink together after
(LCM of 60/7 , 120/13) = 120sec = 2 min,
So in one hour they blink together = 60/2=30 times.
-
Question 2 of 5
2. Question
If a three digit number having no zero, “PQR” is divisible by 3 and another three digit number “PRQ’ is divisible by 6, then what is the minimum value of P+Q+R?
Correct
Solution (a)
Since PQR is divisible by 3 hence P+Q+R must be divisible by 3.
Now PRQ is divisible by 6 which means the number PQR is an even number
Because for it to be divisible by 6, it should be divisible by 2 and 3 first
The minimum value of three digit number PQR=123, and the PRQ=132.
So the sum of digits is 6.
Incorrect
Solution (a)
Since PQR is divisible by 3 hence P+Q+R must be divisible by 3.
Now PRQ is divisible by 6 which means the number PQR is an even number
Because for it to be divisible by 6, it should be divisible by 2 and 3 first
The minimum value of three digit number PQR=123, and the PRQ=132.
So the sum of digits is 6.
-
Question 3 of 5
3. Question
When we reverse the digits of the number 13 the number increases by 18. How many other two-digit numbers are there which increases by 18 when its digits are reversed?
Correct
Solution (a)
Let the numbers are in the form of (10x+y), so when the digits of the number are reversed the number becomes (10y+x).
According to question,
(10y+x) – (10x+y) = 18;
9(y-x) = 18; →y-x = 2.
So, the possible pairs of (x, y) are (1, 3), (2, 4), (3, 5), (4, 6), (5, 7), (6, 8) and (7, 9).
But, we need the number other than 13.
Thus, there are 6 possible numbers i.e. 24, 35, 46, 57, 68, 79.
So, total numbers of possible numbers are 6.
Incorrect
Solution (a)
Let the numbers are in the form of (10x+y), so when the digits of the number are reversed the number becomes (10y+x).
According to question,
(10y+x) – (10x+y) = 18;
9(y-x) = 18; →y-x = 2.
So, the possible pairs of (x, y) are (1, 3), (2, 4), (3, 5), (4, 6), (5, 7), (6, 8) and (7, 9).
But, we need the number other than 13.
Thus, there are 6 possible numbers i.e. 24, 35, 46, 57, 68, 79.
So, total numbers of possible numbers are 6.
-
Question 4 of 5
4. Question
Find the missing number
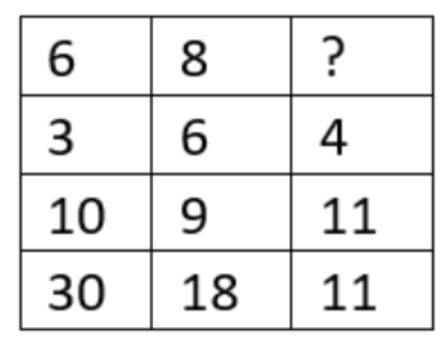 Correct
Correct
Solution (b)
In column I; (6-3)×10 =30
In column II; (8-6)×9=18
Therefore In column III; (5-4)×11=11
Incorrect
Solution (b)
In column I; (6-3)×10 =30
In column II; (8-6)×9=18
Therefore In column III; (5-4)×11=11
-
Question 5 of 5
5. Question
A person employed a group of 20 men for a sales job. These 20 men working 8 hours a day can complete the job in 28 days. The work started on time but after 18 days, it was observed that two thirds of the work was still pending. To avoid penalty and complete the work on time, the employer had to employ more men and also increase the working hours to 9 hours a day. Find the extra men employed if the efficiency of all men is same.
Correct
Solution (c)
Let the total work be 3 units and additional men employed after 18 days be ‘x’.
Work done in first 18 days by 20 men working 8 hours a day = (1/3) x 3 = 1 unit
Work done in last 10 days by (20 + x) men working 9 hours a day = (2/3) x 3 = 2 unit
Here, we need to apply the formula M1 D1 H1 E1 / W1 = M2 D2 H2 E2 / W2, where
M1 = 20 men D1 = 18 days H1 = 8 hours/day W1 = 1 unit
E1 = E2 = Efficiency of each man
M2 = (20 + x) men D2 = 10 days H2 = 9 hours/day W2 = 2 unit
So, we have
20 x 18 x 8 / 1 = (20 + x) x 10 x 9 / 2
x + 20 = 64
x = 44
Therefore, additional men employed = 44
Incorrect
Solution (c)
Let the total work be 3 units and additional men employed after 18 days be ‘x’.
Work done in first 18 days by 20 men working 8 hours a day = (1/3) x 3 = 1 unit
Work done in last 10 days by (20 + x) men working 9 hours a day = (2/3) x 3 = 2 unit
Here, we need to apply the formula M1 D1 H1 E1 / W1 = M2 D2 H2 E2 / W2, where
M1 = 20 men D1 = 18 days H1 = 8 hours/day W1 = 1 unit
E1 = E2 = Efficiency of each man
M2 = (20 + x) men D2 = 10 days H2 = 9 hours/day W2 = 2 unit
So, we have
20 x 18 x 8 / 1 = (20 + x) x 10 x 9 / 2
x + 20 = 64
x = 44
Therefore, additional men employed = 44











