IASbaba’s Daily CSAT Practice Test
ARCHIVES
Daily CSAT Practice Test
Everyday 5 Questions from Aptitude, Logical Reasoning, and Reading Comprehension will be covered from Monday to Saturday.
Make the best use of the initiative. All the best!
To Know More about Ace the Prelims (ATP) 2021 – CLICK HERE
Important Note:
- Don’t forget to post your marks in the comment section. Also, let us know if you enjoyed today’s test 🙂
- After completing the 5 questions, click on ‘View Questions’ to check your score, time taken and solutions.
Test-summary
0 of 5 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
Information
To view Solutions, follow these instructions:
- Click on – ‘Start Test’ button
- Solve Questions
- Click on ‘Test Summary’ button
- Click on ‘Finish Test’ button
- Now click on ‘View Questions’ button – here you will see solutions and links.
You have already completed the test before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the test.
You have to finish following test, to start this test:
Results
0 of 5 questions answered correctly
Your time:
Time has elapsed
You have scored 0 points out of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- Answered
- Review
-
Question 1 of 5
1. Question
Find the sum of all 2-digit numbers that gives a remainder of 3 when they are divided by 7
Correct
Solution (a)
The two-digit number which gives a remainder of 3 when divided by 7 are
10, 17, 24…….94
These number are in AP series with a = 10 and L = 94 with common difference d = 7
Number of terms n = 13
Sum = n*(a + L)/2
Sum = 13*52 = 676
Incorrect
Solution (a)
The two-digit number which gives a remainder of 3 when divided by 7 are
10, 17, 24…….94
These number are in AP series with a = 10 and L = 94 with common difference d = 7
Number of terms n = 13
Sum = n*(a + L)/2
Sum = 13*52 = 676
-
Question 2 of 5
2. Question
Find the missing number from the following pattern
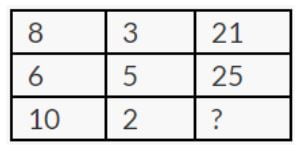Correct
Solution (b)
Column-Wise
(First Column Element * 2nd Column element) – (2nd column element) = Last Column Element
8×3-3=24-3=21
6×5-5=30-5=25
10×2-2=20-2=18
Incorrect
Solution (b)
Column-Wise
(First Column Element * 2nd Column element) – (2nd column element) = Last Column Element
8×3-3=24-3=21
6×5-5=30-5=25
10×2-2=20-2=18
-
Question 3 of 5
3. Question
The two numbers are in the ratio 3:4. If their LCM is 360, Find the smallest number?
Correct
Solution (c)
Let, these two numbers be 3X and 4X then their LCM = 12X.
Now, according to question,
12X = 360;
Or, X = 30;
Thus, the numbers are (3X = 3*30) = 0 and (4X= 4*30) = 120.
Then smaller in this two is 90.
Incorrect
Solution (c)
Let, these two numbers be 3X and 4X then their LCM = 12X.
Now, according to question,
12X = 360;
Or, X = 30;
Thus, the numbers are (3X = 3*30) = 0 and (4X= 4*30) = 120.
Then smaller in this two is 90.
-
Question 4 of 5
4. Question
There are 154 pearls in a necklace, and all are coloured either red or blue or green. The number of blue ones is three less than red and five more than green. Find the number of red pearls?
Correct
Solution (d)
Let the number of red pearls = X.
Hence, Blue pearls = (X-3).
and Green pearls = (X-8).
According to the sum,
X+X-3+X-8 = 154.
3X-11 = 154.
X = 55.
Incorrect
Solution (d)
Let the number of red pearls = X.
Hence, Blue pearls = (X-3).
and Green pearls = (X-8).
According to the sum,
X+X-3+X-8 = 154.
3X-11 = 154.
X = 55.
-
Question 5 of 5
5. Question
Two trains running in opposite directions cross a man standing on the platform in 27 seconds and 17 seconds respectively and they cross each other in 23 seconds. Find the ratio of their speed?
Correct
Solution (a)
Let the speeds of the two trains be X m/sec and Y m/sec respectively.
Then, length of the first train = 27X metres,
and length of the second train = 17Y metres.
27X+17Y/(X+Y) = 23
27X + 17Y = 23X + 23Y
4X = 6Y
Therefore, X/Y = 3/2
Incorrect
Solution (a)
Let the speeds of the two trains be X m/sec and Y m/sec respectively.
Then, length of the first train = 27X metres,
and length of the second train = 17Y metres.
27X+17Y/(X+Y) = 23
27X + 17Y = 23X + 23Y
4X = 6Y
Therefore, X/Y = 3/2
